Richard A. Schmidt

• provided definition of motor learning
• developed schema theory of motor learning

---

Schmidt's definition of motor learning: "Motor learning is a set of [internal] processes associated with practice or experience leading to relatively permanent changes In the capability for responding" (Schmidt, 1988, p.346; Schmidt, 1991, p.51). appears in: Schmidt, R.A. (1988). Motor Control and Learning: A Behavioral Emphasis. 2nd ed. Champaign, IL: Human Kinetics. and in a very accessible article in which Schmidt relates his work to physical therapy: Schmidt, R.A. (1991). Motor learning principles for physical therapy. In: Foundation for Physical Therapy. Contemporary Management of Motor Control Problems: Proceedings of the II-STEP Conference. Alexandria, VA: Foundation for Physical Therapy.

---

R.A. Schmidt developed the "schema theory" of motor learning

Schmidt argued, partly against J.A. Adams'(1971) closed loop theory, that people don't learn specific movements. Instead, they construct "generalized motor programs." They do this by exploring programming rules, learning the ways in which certain classes of movement are related. Then they learn how to produce different movements within a class by varying the parameters that determine the way in which movements are constructed.

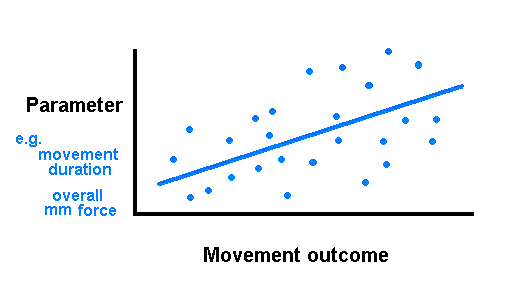
	Parameters are features of a movement, for instance, its duration or overall time, or the level of force that develops in the muscles that contribute to the movement. By scaling these parameters up or down (vertical axis), people produce variations (horizontal axis) among a class of movements.

As people practice a movement, like throwing a ball various distances or in various directions, or climbing stairs of various dimensions, they learn the relationship between the parameters and the outcome. By collecting "data points" like the ones in the figure (adapted from Schmidt, 1988, Fig. 14-7), they improve their understanding of the relationship between a movement outcome and their control of the movement's parameters (the "best-fitting straight line" in the figure).

An important prediction of the theory is that people will more quickly learn the relationship between manipulating parameters and achieving a desired movement outcome if they practice a task in wide variety of sitations, and experience errors in the process. To use the figure as an illustration, the theory predicts that people will more quickly appreciate the underlying "best-fitting line" (the rules by which a generalized motor program produces a class of movements) when they accumulate a large and broad scatter of data points (a varied experience of movement).

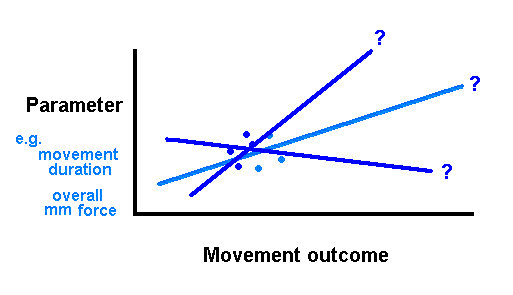
	Practice that lacks variety, but is instead precise or repetitious, will not (from Schmidt's perspective) provide enough information for a learner to fathom the rules that underlie the generalized motor program.

In Schmidt's theory, this relationship betweeen the parameters and outcomes are collected in two "schemes" or "schema," hence the name by which his theory is known.

• Recall schema relates outcomes to parameters like those listed above, movement duration, overall force production, etc.

• Recognition schema relates expected sensory consequences of a movement to the movement's outcome. This is reminiscent of Adams' earlier ideas of an "internal reference of correctness"

Schmidt describes the theory's main points in:

Schmidt, R.A. (1988). Motor Control and Learning: A Behavioral Emphasis. (2nd ed.). Champaign, IL: Human Kinetics, pp. 482-489. The seminal article is:

Schmidt, R.A. (1975). A schema theory of discrete motor skill learning. Psychological Review, 82, 225-260.

Last updated 5-2-01 ©Dave Thompson PT
return to Motor teaching and motor learning