
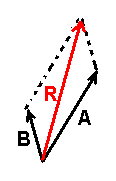
Two equivalent techniques exist for vector composition. We can add vectors in a "head-to-tail" manner or by using a "parallelogram" method. To employ the latter method, we must draw two individual vectors with a common point of application, then construct a parallelogram whose diagonal is the sum or resultant of the two vectors.
The figures below demonstrate these two techniques for determining a resultant vector (R) formed from individual vectors (A and B).

| 
|
|---|---|
HEAD-TO-TAIL COMPOSITION PARALLELOGRAM COMPOSITION |
Note that the magnitude and direction of vectors A and B, hence the magnitude and direction of their resultant R, is unaffected by the choice of technique.
Problems:
| View a commentary on this problem. |
|---|
| Hint: Use the parallelogram method, drawing both vectors with a common point of application near the patella's center. To draw vectors with a common point of application, it is permissible to "slide" either one along its respective line of application.View commentary on this problem. |
|---|
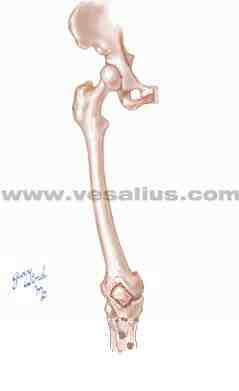
| Hint: a line that connects the superior patellar pole with the ASIS is an acceptable approximation of the line of application of a vector that depicts the overall force of the four quadriceps muscles.View a commentary on this problem. |
|---|
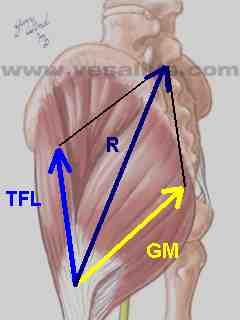
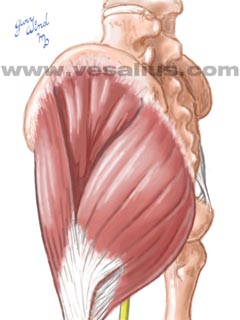
| The gluteus maximus (one of whose many lines of application is depicted by vector GM) and the tensor fascia latae (similarly depicted by vector TFL) attach to the iliotibial band. Using the paralellogram method, and placing the muscle's common point of application on the iliotibial band, we can construct a resultant vector R. |
|---|
Were we to illustrate the synergy in the frontal plane, we would discover that the two muscles both the TFL and the superior fibers of the gluteus maximus produce abduction, the resultant vector would produce a large abductor moment around the hip's antero-posterior (AP) axis.
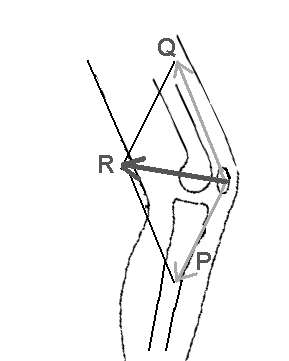
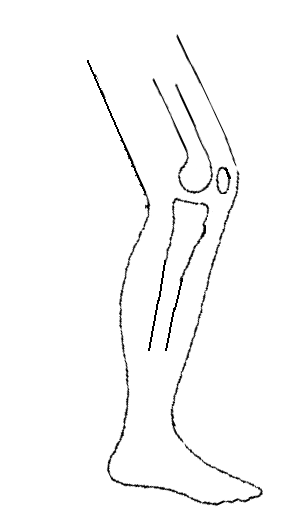
| The patella "feels" a superior pull from the quadriceps muscles (vector Q). However, it doesn't move superiorly because another force restrains it. Tension in the patellar tendon (vector P) simultaneously pulls the patella inferiorly. Because the patella remains stationary, and because that tension within a muscle-tendon structure must be equal throughout that structure's length, these two forces must be roughly equal. Accordingly, we draw their vectors of equal length. |
|---|
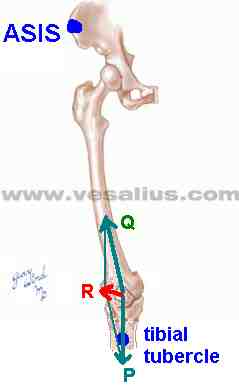
| The quadriceps exert a force on the patella in the direction of the ASIS (vector Q). The patella doesn't move superiorly because another force, that of the patellar tendon (vector P), restrains it. Force or tension within the quadriceps' muscle-tendon structure must be equal throughout that structure's length. Therefore, forces Q and P are equal in magnitude and their vectors are equal in length. The result of vector composition is a resultant (vector R) force that tends to pull the patella laterally. |
|---|
The degree to which quadriceps forces pull the patella laterally depends on the body's structure, which affects the q-angle. Lateral patellar subluxation is prevented by tensile forces in medial structures like the medial patellar retinaculum, and by resistance to compression in lateral structures like the lateral femoral condyle.