Modeling human tissues as springs:

A spring or, analogously, a muscle or ligament, develops force as it is elongated. The force it develops comes from three sources:
  1. Inertial forces
  2. Elastic forces
  3. Viscous forces

  1. Inertial forces

    A mass at rest tends to remain at rest; it resists being accelerated.

    Fi=ma
    where Fi is inertial force
    m is the structure's mass
    a is the acceleration (d2l/dt2) at which the structure elongates
    dl=L-l0

  2. Elastic forces

    Springs store energy as they are elongated. The elastic force they store varies directly with the distance they are elongated beyond their resting length l0.

    Fe = E * dl
    where Fe is elastic force
    E is a measure of the spring's (tissue's) stiffness
    dl=L-l0

  3. Viscous forces

    The molecular structure of many tissues causes them to display the property of viscosity, a resistance to flow, that many therapists call "damping." In these tissues, stiffness (the slope of the passive length-tension curve) increases when the rate (or velocity) of elongation increases.

    Fv = N * d(dl)/dt
    where Fv is viscous force
    N is a measure of the spring's (tissue's) viscosity or damping property
    dl=L-l0
    d(dl)/dt is the velocity or time rate of elongation

    Human tissues appear solid. To understand how they might possess properties, like viscosity, that relate to flow, we recall that their protein molecules move with respect to each other in an aqueous environment. At the level of the protein molecules that comprise muscle fibers, the formation of transient cross-bridges may explain another property, thixotropy, which may contribute to muscle's viscoelastic behavior.

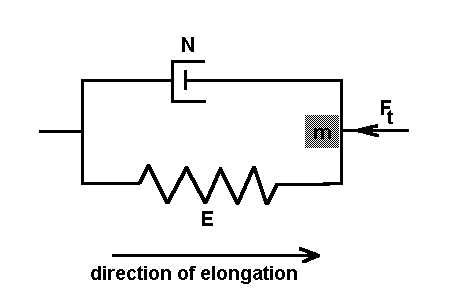
    The passive force that develops in an elongating tissue is the sum of inertial, elastic, and viscous effects.

    Ft

    = Fi + Fe + Fv

    = ma + (E * dl) + (N * d(dl)/dt)

    In a tissue that elongates at a fairly constant rate (so the acceleration a is close to zero), we can ignore the contribution of inertial force (ma).

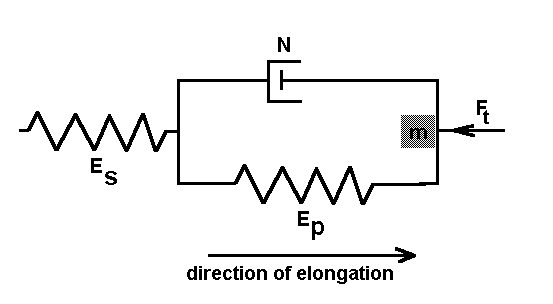
    hill model

    Some spring models differentiate between series and parallel elements. Magnusson, Simonsen, Aagaard, Kjaer (1996) discuss research that attributes a muscle's series elastic properties (Es) to the endomysium, and its parallel-elastic properties (Ep) to the perimysium.

    Viscoelastic tissues illustrate DIFFERENT length-tension behavior when they are passively loaded (subjected to stress) than when they are unloaded.
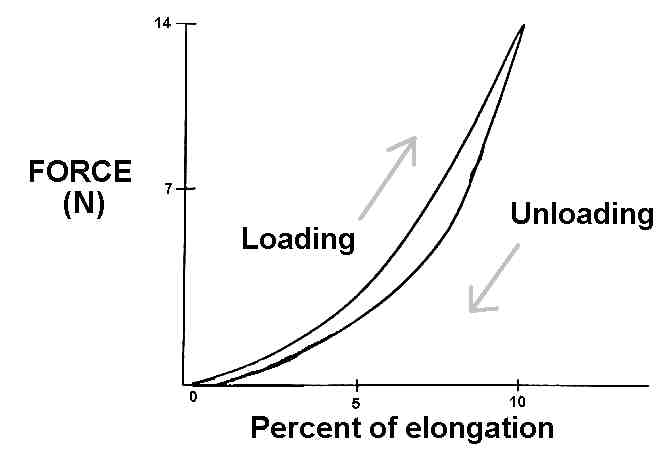
    hysteresis loop

    These tissues' length-tension curves differ for loading and unloading. This graph (Rodgers & Cavanagh, 1982) illustrates this property of HYSTERESIS.

    Reference: Magnusson, S.P., Simonsen, E.B., Aagaard, P., & Kjaer, M. (1996). Biomechanical responses to repeated stretches in human hamstring muscle in vivo. American Journal of Sports Medicine, 24, 622-628.

    Rodgers, M.M., & Cavanagh, P.R. (1984). Glossary of biomechanical terms, concepts, and units. Physical Therapy, 64, 1886-1902.

    Last updated 1-18-00 Dave Thompson PT