Interaction Torques

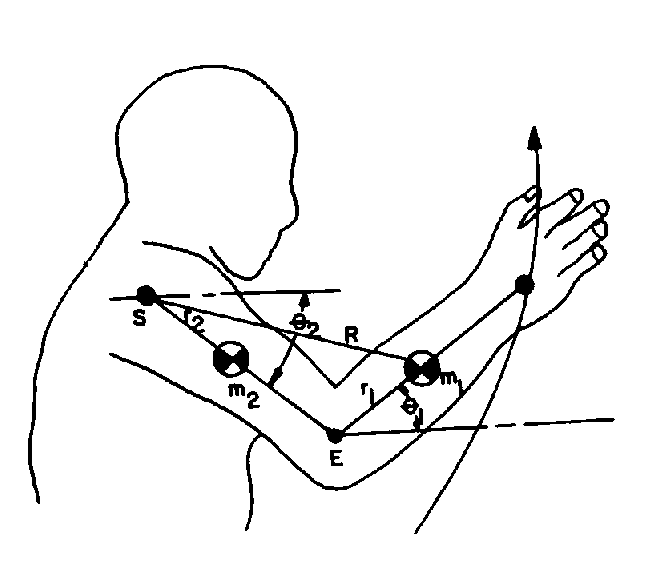
Static or quasi-static analyses are adequate for movements that are relatively slow or that involve a single joint. When we consider movements that are rapid or that involve a kinetic chain of several joints, we must consider "interaction torques" or "motion dependent torques." These torques are of three varieties: inertial torques centripetal torques coriolis torques

1. inertial (or tangential) forces and moments (torques)

   F_i=ma

   F_i=mra if a is expressed in radians/sec²

   When a multijoint kinetic chain moves, a segment’s movement is affected by movement at the other "distant" joints in the chain. Each of those moving joints contributes an inertial torque to the other joints in the chain.

   Thus, the inertial torque M_i = F_ir = mr²a. This torque is a function of:

   1. the angular acceleration of the "distant" moving joint
   2. the moment of inertia of those segments distal to both joints

   centripetal (or radial) forces and moments

   F_cn=ma
   where a is directed away from the joint center and is equal to
   a=v²/R

   If v is expressed in radians/sec², then
   F_cn=mv² and
   the centripetal moment M_cn=F_cnR

   where R is the perpendicular moment arm from the force's line of application to the joint center.

   In the diagram above, shoulder movement produces centripetal forces at both the shoulder and the elbow.

   Coriolis forces and moments

   If two joints in a kinetic move at different angular velocities, they produce a separate Coriolis force whose magnitude is proportional to the difference between their velocities

   The coriolis force (C) that acts on the more distal of the two segments is:

   C= 2*v₁*v₂*r₁*m₁

   web resources that explain Coriolis forces:

   • Univ. of Montana Dept. of Mathematics
   • Dave Van Domelen, Ohio State Univ. Dept. of Physics
   • "first millenial foundation
   • Earth Space Research Group, U. Cal. Santa Barbara
   • Dept. of Atmospheric Sciences, Univ. Ill, Champaign-Urbana

---

Other sources of information on interaction forces and moments:

• Hollerbach, M.J., & Flash, T. (1982). Dynamic interactions between limb segments during planar arm movement. Biological Cybernetics, 44, 67-77.

• Chaffin DB, Andersson GB. Occupational Biomechanics. pp.202ff.

• Hennion, P.Y., & Mollard, R. (1993). An assessment of the deflecting effect on human movement due to theCoriolis inertial forces in a space vehicle. Journal of Biomechanics, 26, 85-90.

• Hooper HO, Gwynne P. Physics and the Physical Perspective. 2nd ed. San Francisco: Harper and Row,1980:101-102.)

• Konczak J., Borutta M., Topka H., Dichgans J. (1995). The development of goal-directed reaching in infants: Hand trajectory formation and joint torque control. Experimental Brain Research. 106, 156-68.

• Lackner, J,R., & Dizio, P. (1994). Rapid adaptation to Coriolis force perturbations of arm trajectory. Journal of Neurophysiology, 72, 299-313.

• Perell, K.L., Gregor, R.J., Buford, J.A., & Smith, J.L. (1993). Adaptive control for backward quadrupedal walking. IV. Hindlimb kinetics during stance and swing. Journal of Neurophysiology, 70, 2226-40.

• Putnam, C.A. (1993). Sequential motions of body segments in striking and throwing skills: Descriptions and explanations. Journal of Biomechanics, 26 Suppl 1, 125-35.

• Sainburg, R.L., Ghilardi, M.F., Poizner, H., & Ghez, C. (1995). Control of limb dynamics in normal subjects and patients without proprioception. Journal of Neurophysiology,73,820-35.

• Zernicke RF, Schneider K. Biomechanics and developmental motor control. Child Development. 1993;64:982-1004.

---

Last updated 3-31-00
Dave Thompson PT