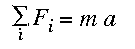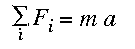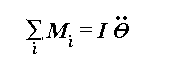Equilibrium of forces and moments
When one force acts on mass, we can apply Newton's Law:
F=ma
When several forces act on a mass, we simply sum their individual effects on the mass:
F1 + F2 + F3 + F4 + ... Fn=ma
Thus,
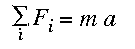
Similarly, we can analyze the effects of several moments of force around an axis of movement:
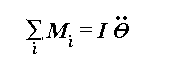Where the total moment equals the product of I, the segment's moment of inertia around an axis of movement, and its angular acceleration around that axis.
Static equilibrium
We refer to a situation as static when a mass' acceleration (j in the equation above), either in a straight line or around a joint axis, is equal to zero, or very nearly zero. Acceleration is zero when the mass is at rest, that is, not moving or moving at a constant velocity.
In this case, the equation that defines static equilibrium is:
EM=0
and the sum of the moments acting around a joint axis is zero. For example, in this frontal plane view of the lower extremity,
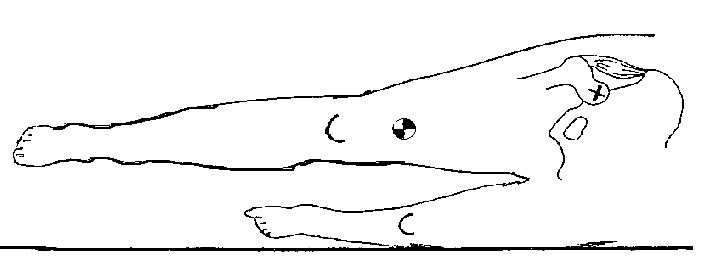
the sum of moments producing hip adduction are perfectly balanced by moments that produce hip abduction.
Thus,
Mm = Mg
Fgsg=Fmsm
Fm = (Fgsg)/sm
Dynamic Equilibrium
We often treat movement problems as if they are static, assuming that accelerations are nearly zero.
These assumptions make movement problems easy to solve. When these simplifying assumptions are unwarranted, when a joint does not move at a constant velocity (including v=0) and an angular acceleration equal to zero, we must deal with the more complex equilibrium equation:
EM=Ij
where the total moment that acts on the joint (EM, the sum of individual moments) is measurable and nonzero.
| Total moment = | (internal) joint moment
- gravity moment
- interaction moments
|
|---|
The joint moment is calculated as a residual once the other moments are known:
| Joint moment = | Total joint moment
+ gravity moment
+ interaction moments
|
|---|
Where
- Total moment is the product of the joint angular acceleration and the segment's moment of inertia about the joint.
- Gravity moment is that produced by gravity acting on the segment center of mass
- Interaction moments or torques include those produced by inertial, centripetal, and coriolis forces.