Gravity's (body weight's) effect on the hip joint surface during unilateral stance

Using the technique of vector resolution, we can analyze the effects that gravitational forces have on the hip's articular surfaces.

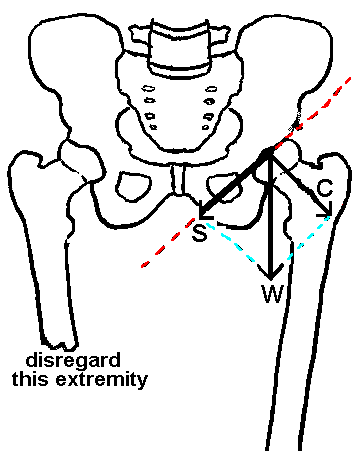
We begin by drawing a red, dashed reference line that approximates the hip joint surface's orientation. The surface is curved, so we estimate the orientation of a line that is tangent to that curve.

frontal plane view of hip

Vector W represents the force of gravity acting on the body mass that is superincumbent to the hip joint. To analyze vector W's effect at the joint surface, we have translated it through space until its point of application lies on the reference line. The vector's exact placement on the reference line is unimportant as long as we neither "tip" (angulate) the vector nor change its magnitude (length) during the translation. Of course, once we move the vector from its original location, we can no longer use it to measure moment arms, but that is not our purpose.

Instead, our purpose is to understand how gravity's force affects the joint surface. To accomplish this, we resolve gravity's force into two component forces, both of which act at right angles to one another:

  1. a component that lies at a right angle to the reference line. This is vector C, so named here because it demonstrates how much of gravity's force, acting on the pelvis and superincumbent mass, produces compression between the pelvis and the femoral head.

  2. a component that lies directly on the reference line. This is vector S, so named here because it represents a shear force, a force that produces a sliding along the joint surface. This vector's medial direction demonstrates that gravity causes the acetabulum to slide medially on the femoral head.

It takes some practice to learn how long to draw the component vectors. The finished product should look like the figure, with the component vectors drawn just long enough so the original vector is actually their resultant. (Vector resolution is a reciprocal operation to vector composition, much like division is a reciprocal arithmetic operation to multiplication.)

The same analysis clarifies the effects on the hip joint surface of the abductor muscles.

Last updated 7-9-00 ©Dave Thompson PT